确定磁场最小面积历来是高考中的重点和难点，其实它的知识点已经包含在我们前面阐述的内容中了。下面结合例题介绍几何方法。

例1.一质量为m、电荷量为+q的粒子以速度v，从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从b处穿过x轴，速度方向与x轴正方向的夹角为30°，同时进入场强为E、方向沿与x轴负方向成60°角斜向下的匀强电场中，通过了b点正下方的c点，如图所示，粒子的重力不计，

试求：（1）圆形匀强磁场区域的最小面积；（2）c点到b点的距离。

解析：

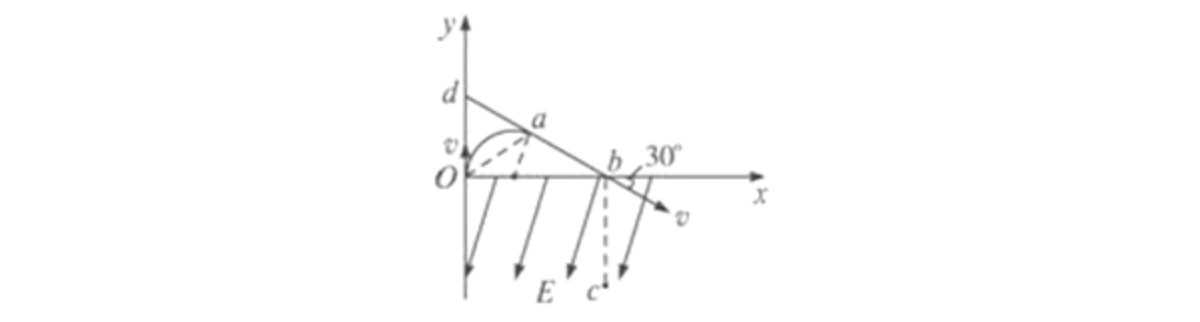
传统方法在任何时候都是我们解题的首选。所以先找圆心（三种方法你还都记得吗？），显然本题的圆心在x轴正半轴上。那么最小磁场该如何构造呢？我们可以大概画一个普通圆试一下，很明显就会发现这是变向考察圆和直线的关系，相切最小。所以过b点逆着速度v的方向作直线bd，交y轴于d，由于粒子在磁场中偏转的半径一定，且圆心位于Ob连线上，距O点距离为圆的半径，易得R=mv/qB，过圆心作bd的垂线，粒子在磁场中运动的轨迹如图所示，Oa为圆形磁场的一根弦。要使磁场的区域有最小面积，则Oa应为磁场区域的直径，由几何关系知：r=Rcos30°。其他就不再赘述了。第二问作为复合场后续再说。

反思：圆心、半径、轨迹在解题中必不可少，圆形磁场区域的最小面积往往是由运动轨迹上任意两点的弦恰好是半径时最小。

例2如图所示，

直角坐标系xoy，第一象限的区域存在沿y轴正方向的匀强电场。现有一质量为m，电量为e的电子从第一象限的某点（L，√3/8L）以初速度v沿x轴的负方向开始运动，经过轴上的Q点（L/4，0）进入第四象限，先做匀速直线运动然后进入垂直纸面的矩形匀强磁场区域，磁场左边界和上边界分别与y轴、x轴重合，电子偏转后恰好经过坐标原点O，并沿y轴的正方向运动，不计电子的重力。求（1）电子经过点Q的速度；（2）该匀强磁场的磁感应强度和磁场的最小面积。

解析：电子从点开始在电场力作用下作类平抛运动运动到点，我想这方面内容只要你好好学习过，应该没有什么问题。在此不再赘述。由第一问我们可以知道经过Q点后，带电粒子以与水平方向负半轴方向成30º角的方向射入第四象限。先做匀速直线运动，再匀速圆周运动，看起来不太好想或者不太好画。此时我们可以先画轨迹圆。如图所示。

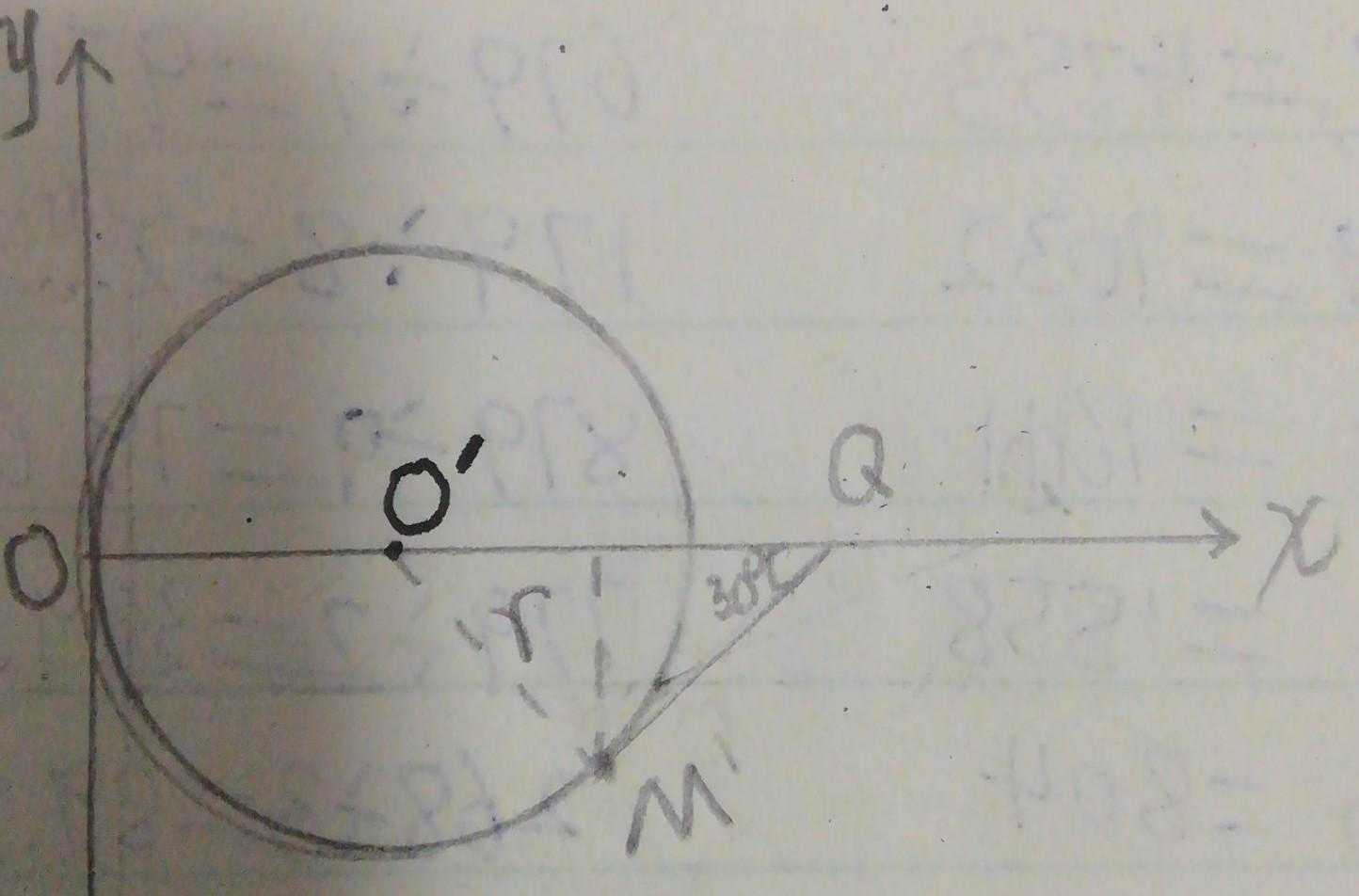
画完轨迹后，我们看题意，粒子过原点且向竖直正方向射出，所以轨迹圆的圆心O'一定在x轴上，匀速直线运动的方向显然与轨迹圆相切时面积最小，所以自然再画切线与水平方向的交点就是Q点。通过几何关系其他就不难求出。

反思：本题虽然冠以矩形之名，其实解题思路还是和上题如同一辙，均是直线与轨迹圆相切。只不过需要倒着画图更简单一些而已。

例3一个质量为m，带+q电量的粒子在BC边上的M点以速度垂直于BC边飞入正三角形ABC。为了使该粒子能在AC边上的N点（CM＝CN）垂真于AC边飞出ABC，可在适当的位置加一个垂直于纸面向里，磁感应强度为B的匀强磁场。若此磁场仅分布在一个也是正三角形的区域内，且不计粒子的重力。试求：（1）粒子在磁场里运动的轨道半径ｒ及周期T；（2）该粒子在磁场里运动的时间t；（3）该正三角形区域磁场的最小边长；

解析：有没有读完题就想把C点当做圆心的冲动？冲动是魔鬼啊，一定要先判断受力，再看运动情况。令人崩溃的是一进去就受到向左的力。怎么办？还是反推比较简单。先画圆，看粒子怎么样就可以实现如此方向，如图

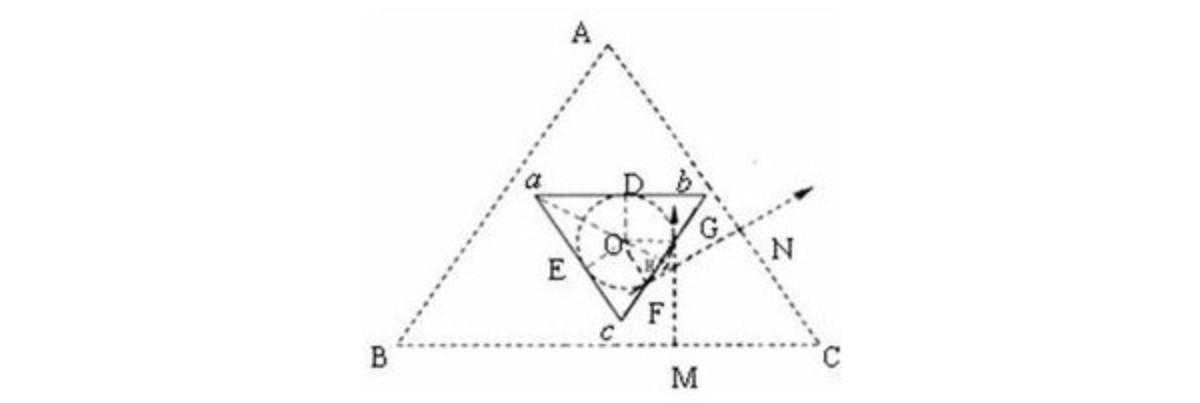
确定磁场入射点和射出点后，画复合条件的三角形磁场区域。显然，aH为底边cb上的高，aH=aO+OH=2r+rcos30°。其他就可以迎刃而解了。

反思：如果不是先画圆，这道题中粒子运动轨迹和磁场边界临界点的确定比较困难。另外，切记不能想当然，在计算最小边长时一定要注意圆周运动的轨迹并不是三角形磁场的内切圆。