【题目】：如下图，点P是∠AOB内的一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=3√2，则△PMN的周长的最小值是多少？

〖分析与解答〗：此题是求3条线段长度和的最小值，按照常规思路，我们首先要将3条线段顺到一条边上，可以试着分别找到P点关于OM、ON的对称点，如下图：

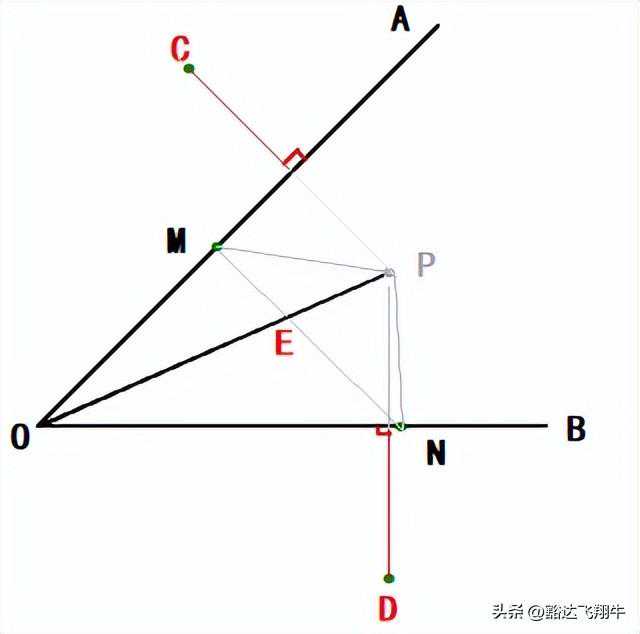
这样一来，PM=CM、PN=DN；然后分别连接OC、OD、CD，如下图：

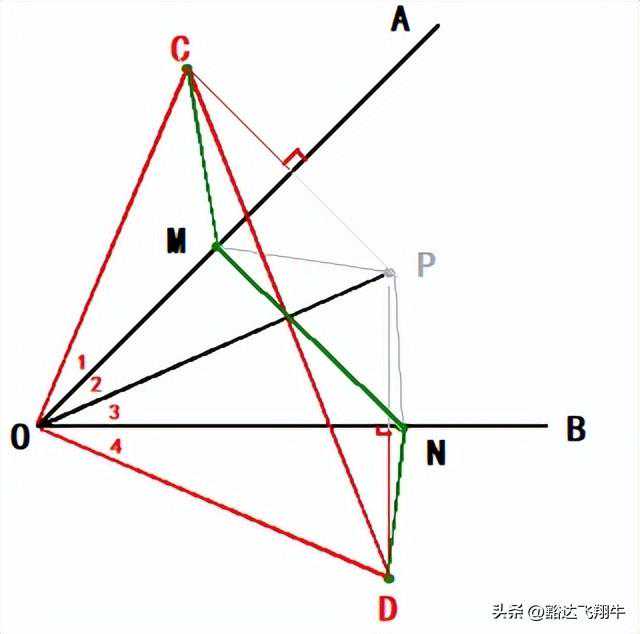
此时，△PMN的周长被顺到了CMND这条折线上，△PMN的周长=CM+MN+ND，很明显，当四点共线时，△PMN的周长=CM+MN+ND=CD最短。CD怎么计算呢？很明显，△COD是一个等腰直角三角形，已知两条直角边=OP=3√2求斜边，斜边CD=√2×OP＝√2×3√2＝6,故△PMN的周长的最小值是6.

〖小结与讨论〗：此题是比较简单的求最值问题，我们运用的是常规思路来解答，您是否还有更简捷的解法可以分享？另外本题擂台赛冠军依然是北京网名为“VIP8905208”的读者(六连冠)，特此嘉奖：

【擂台№63】：如下图，等边△ABC的边长为3，E、D分别在AB、BC边上，且AE=BD，则BM的最小值是多少？

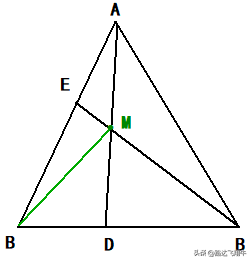
【备注：此题分析解答下期给出】